HADES PROTOCOL
A non-federated cryptographic protocol for end-to-end encrypted communication in the Metaverse
Security is not guaranteed; Use at your own peril
Vulnerabilities may lurk in the protocol and/or implementation(s)
Introduction
A while back I decided that maybe this Metaverse thing should be taken a little bit more seriously. It's not unreasonable to assume that virtual/augmented reality based experiences will get more popular, if not become the primary way through which the average Joe consumes his content. Nor would it be prudent to allow large corporations to dominate the space with their privacy-invasive proprietary solutions, or the greedy "Web 3.0" companies that insist on their clunky and superfluous blockchain integrations. So I wrote down the design of this new protocol that I came up with, and programmed two implementations (client and server). Sadly I'm no cryptographer, so expect design errors and security vulnerabilities.
The gist of the protocol is that in the Metaverse there are mainly two kinds of data that require encryption: individually-owned data such as the voice and position of the avatar, and collectively-owned data which is the sort of data that multiple users are allowed to modify (either simultaneously or not). For a game of chess, the position of the board would be collectively-owned, since both players are allowed to move the pieces (under some rules!), but when one of the players speaks, his/her speech cannot be changed by the other player (i.e. speech is individually-owned). The protocol is designed around this dichotomy.
Core Cryptography
The protocol uses the following schemes:
-
Key Exchange:X25519 + Crystals-Kyber-1024 -
Signatures:Ed25519 + Crystals-Dilithium5 -
End-to-End Encryption:ChaCha20-Poly1305 (secret keys derived from HKDF-SHA256) -
Calculations on Encrypted Data:Fully Homomorphic Encryption (in my thesis I used CKKS) -
Hashing:Argon2 for password-hashing and Blake2 for data hashing
Elements
Fundamental structures:
-
{User, Virtual, Public} Identities:JSON-serializable identity objects that carry the cryptographic keys of their owners. -
Hadean Transmission Format (HTF):A slightly modified version of the glTF 2.0 standard with added programmability via the Lua scripting language, Khronos textures, and a new state object to process and transmit {user, collectively}-owned data. Some glTF constructs like cameras and external references are removed. The format is binary-only. -
Local Programmable States (LPS):Allows implementations to process and transmit individually-owned data, e.g. user's voice, movement, etc., encrypted under a chosen AEAD scheme (e.g. ChaCha20-Poly1305). The ciphertexts are non-malleable. -
Shared Programmable States (SPS):Allows implementations to process and transmit collectively-owned data, e.g. the position of the chess board, the physics of the virtual world, etc, encrypted under a chosen FHE scheme (e.g. CKKS). The ciphertexts are malleable. -
Obols:JSON-serializable objects used to initiate sessions (like group chats, but the list of participants is fixed and everyone is online).
E2EE Chess
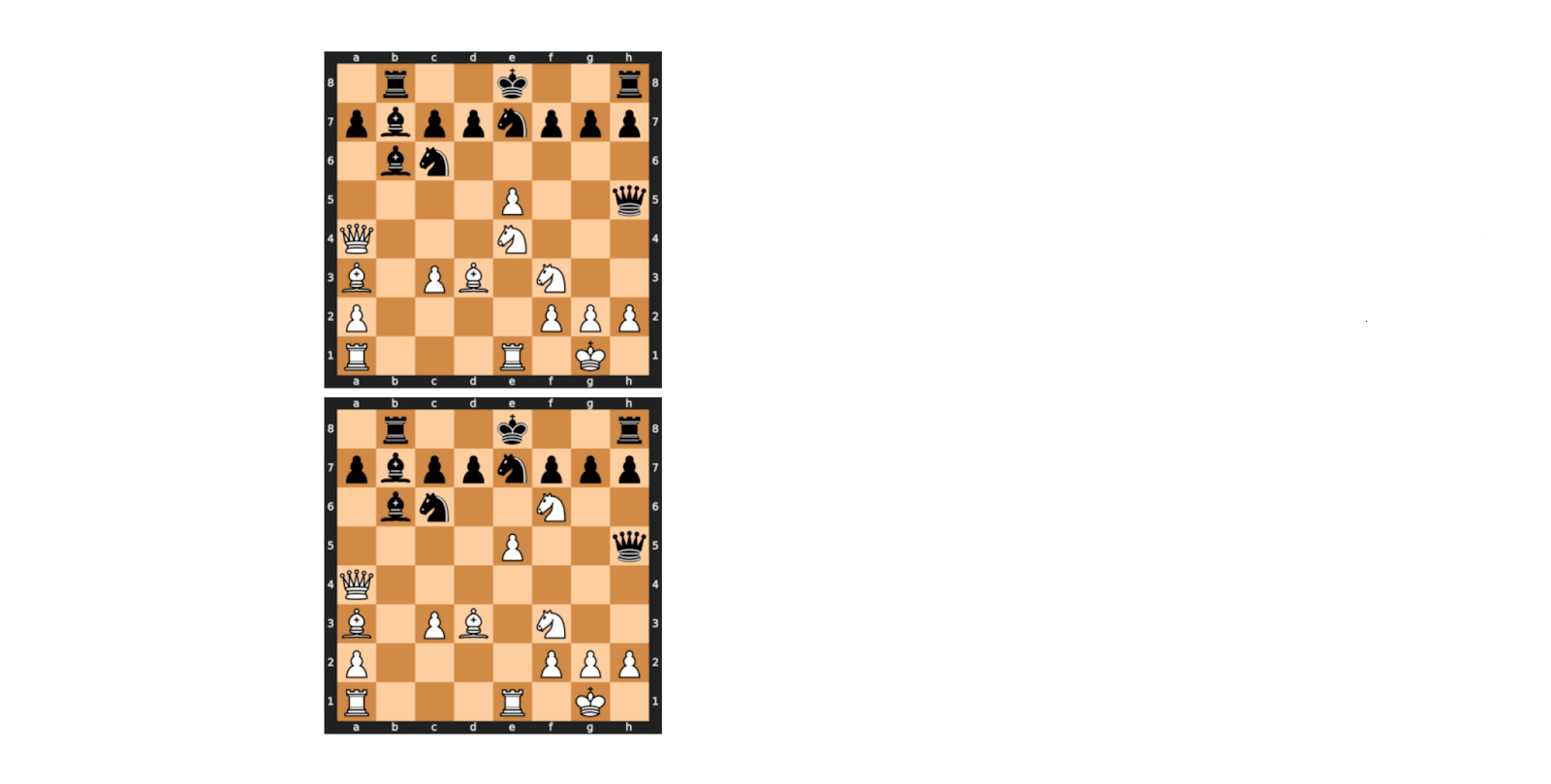
Technically there is a way to run RAM programs on top of FHE, such that the instructions are also encrypted, but I decided to go with the machine-learning (Karpathian) approach. See the figure above. Essentially, each move (represented as the concatenation of board positions before and after the move) is homomorphically-encrypted under a chosen FHE scheme with a secret key SK, and then you run some function 𝓗 on the encrypted input, producing encrypted output, which, when decrypted, reveals whether the move was legal/illegal/checkmate. I named this Programmable Blind Arbitration in the whitepaper, since the arbiter isn't aware of the moves being played (although trainable would be more appropriate here since my arbiter is actually a pre-trained multi-layer perceptron).
This approach has a lot of limitations. Namely, large keys have to be transferred to the server before any blind validation can proceed (about 11 gigabytes worth). Also, the machine-learning approach results in models with many failure cases, some of which are documented both in the whitepaper. In my blog post I experimented with different kinds of models.
Implementations
-
Charon:Client-side implementation (forward+ physically-based bindless renderer written in C++ and powered by Vulkan, with shaders written in Slang) -
Minos:Server-side implementation (multi-threaded server written in C++ that uses OpenFHE for fully-homomorphic encryption)
Links: